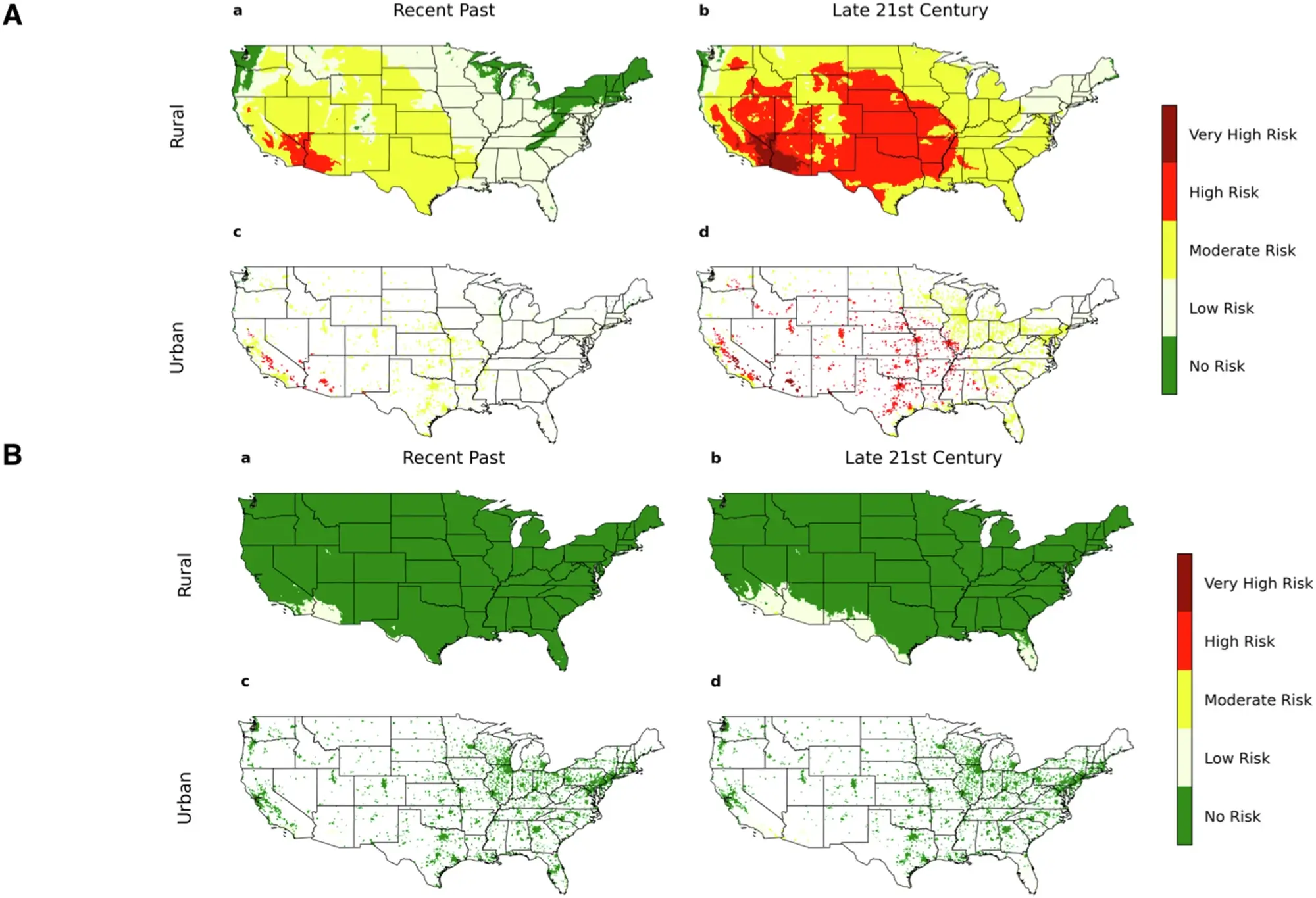
Imagine you’re trying to catch a butterfly in your garden. You see it fluttering around, and you want to know exactly where it is and how fast it’s going. Now, if you get close enough to touch it, the butterfly might flutter away faster or change direction. This is sort of like what happens in the quantum world with the Heisenberg Uncertainty Principle.
What’s the Heisenberg Uncertainty Principle?
The Heisenberg Uncertainty Principle is a fundamental idea in quantum mechanics, which is the science of the very small—like atoms and particles. Named after Werner Heisenberg, who proposed it in 1927, this principle says that you can’t know both the exact position and the exact speed of a particle at the same time.
What exactly is the Heisenberg Uncertainty Principle in the simplest terms?
The Heisenberg Uncertainty Principle states that it’s impossible to simultaneously know both the exact position and the exact momentum of a particle. The more precisely you measure one, the less precise the measurement of the other will be.
Why Can’t We Know Both?
In the world of tiny particles, everything is in constant motion. If you try to measure where a particle is, you’ll change how fast it’s moving. And if you measure how fast it’s going, you’ll disrupt its position. It’s not because our tools aren’t good enough; it’s the nature of things at this scale.
Think of it like trying to see a firefly in the dark. If you shine a light to see where it is, the firefly moves because of the light. Here, the light represents our attempt to measure, and the movement of the firefly shows how our measurement affects the particle.
How Does It Work?
When scientists try to measure a particle’s position, they use photons (which are like tiny packets of light). When these photons hit the particle, they give it a little push, changing its speed. If they try to measure speed, they need to look at the particle over time, which means they can’t pinpoint where it is at any one moment.
The Quantum World vs. Our Everyday World
In our daily lives, this principle doesn’t seem to matter much. You can tell where your car is and how fast it’s going without changing either.
But remember, everything in the universe, including you, is made of particles. When you zoom in to the scale of atoms, the rules change. Here, particles behave like both particles and waves, making everything a bit unpredictable.
Implications of the Uncertainty Principle
This principle isn’t just a cool fact; it has huge implications for science. It tells us that at the core of reality, there’s an inherent unpredictability. It’s why we can’t predict exactly what an electron will do next in an atom or why quantum computers might one day outthink our best traditional computers.
Heisenberg Uncertainty Principle in Real Life Science
This principle affects how we understand and perform experiments in labs. For example, when scientists want to study the behavior of particles in an accelerator, they have to account for this uncertainty. It’s also why we use probability in quantum mechanics rather than definite predictions.
So, the Heisenberg Uncertainty Principle teaches us that in the quantum world, precision has its limits. It’s like a cosmic game of hide and seek where the more you know about one thing, the less you know about another. This isn’t because we’re not smart enough but because nature itself plays by these rules at the smallest scales.
Equation
The mathematical expression for the Heisenberg Uncertainty Principle for position and momentum is:
Δx⋅Δp ≥ ℏ2
Here,
- Δx is the uncertainty in position,
- Δp is the uncertainty in momentum,
- ℏ (h-bar) is the reduced Planck’s constant, approximately 1.054×10−34 Js.
For energy and time, the equation looks like this:
ΔE⋅Δt ≥ ℏ2
Where,
- ΔE is the uncertainty in energy,
- Δt is the uncertainty in time.
Derivations
The derivation of the Heisenberg Uncertainty Principle involves quantum mechanics and the properties of wave functions. Here’s a simplified conceptual derivation:
- Wave-Particle Duality: Particles can be described by wave functions. The position of a particle is related to the wave function’s spread.
- Fourier Transforms: In quantum mechanics, position and momentum are related through Fourier transforms. A very localized wave packet (small Δx) requires a broad range of momentum components (large Δp), and vice versa.
- Mathematical Inequality: Using properties of Fourier transforms, one can show that the product of uncertainties Δx and Δp must be greater than or equal to ℏ2.
Formula
The formula for the uncertainty principle in terms of position and momentum:
Δx⋅Δp ≥ ℏ2
For energy and time:
ΔE⋅Δt ≥ ℏ2
Examples
- Electron in an Atom: An electron in an atom has an uncertain position because it’s not confined to a single point but spread out in an orbital. If we try to measure its position more precisely, we’ll know less about its speed.
- Photons in Light: When light is treated as particles (photons), knowing exactly when a photon arrives (small Δt) means we can’t know its energy precisely (large ΔE), leading to phenomena like the spread of photon arrival times in quantum optics.
Applications
Quantum Mechanics: Fundamental in understanding atomic and subatomic structures.
Quantum Computing: The principle underpins the behavior of qubits, where superposition and entanglement exploit this uncertainty.
Electron Microscopy: Techniques like electron microscopy must account for this principle, as high resolution (small Δx) increases momentum uncertainty, potentially damaging samples.
Spectroscopy: The time-energy uncertainty relation affects how we interpret spectral lines, where short-lived states have broader energy distributions.
FAQs on the Heisenberg Uncertainty Principle
Q: Why is it called the “Uncertainty Principle”?
A: “Uncertainty” here refers to the inherent limitation in our ability to measure certain properties of particles with unlimited precision at the same time. It’s not about our measurement tools being bad; it’s a fundamental property of quantum mechanics.
Q: Who was Heisenberg, and why is it named after him?
A: Werner Heisenberg was a German physicist who formulated this principle in 1927. He’s known for his contributions to quantum mechanics, and this principle is named after him because he was the first to articulate it.
Q: Does this principle apply only to very small things like atoms?
A: Primarily, yes. It’s most noticeable and significant in quantum mechanics, dealing with particles like electrons, protons, or photons. However, the principle is universal; it just doesn’t significantly affect macroscopic objects in everyday scenarios due to the scale.
Q: Can you give a simple example to illustrate this principle?
A: Imagine trying to determine where a tiny dust particle is floating in the air. If you shine a light to see it better (measure its position), you’ll nudge it with photons, changing how fast it’s moving (its momentum).
Q: How does this affect the way scientists study particles?
A: Scientists must design experiments considering this principle. For instance, when studying particle physics, researchers accept that they’re dealing with probabilities rather than certainties, which influences how experimental results are interpreted.
Q: What’s the significance of “h-bar” in the equations?
A: “h-bar” (ℏ) is the reduced Planck’s constant, which is a fundamental constant in quantum mechanics. It relates energy, time, position, and momentum in a way that reflects the scale where quantum effects become significant.
Q: How does this principle relate to quantum computers?
A: Quantum computers use quantum bits (qubits) that can be in superposition, meaning they can represent multiple states at once. The uncertainty principle underpins this behavior, allowing for computational advantages over classical computers.
Q: Can this principle be observed in everyday life?
A: Not directly, because the effects are incredibly small for macroscopic objects. However, the principle influences technologies like electron microscopes or the stability of matter at the atomic level, which indirectly affects our daily lives.
Q: Does this mean the universe is inherently unpredictable?
A: At the quantum level, yes. The principle introduces an intrinsic randomness or unpredictability into the behavior of particles, which is why quantum mechanics deals in probabilities rather than certain outcomes.
Q: Is there any way to “bypass” the Heisenberg Uncertainty Principle?
A: No, it’s a fundamental limit of nature. However, through clever experimental design, scientists can minimize the impact of uncertainty for specific measurements, but the principle itself remains inviolable.